로그 공부하고 뒤에 한 번 보자. 또한 속도 즉 식이 나오는 것을 다시 공부해보자
정렬부터는 알고리즘에 대해서 배운다.
알고리즘(Algorithms)
9세기 페르시아의 수학자 '아부 압둘라 무하마드 이븐 무사 알 콰리즈키의 이름에서 따온 이름
: 문제를 해결하기 위한 일련의 명령이나 반복되는 절차를 말한다.
이번에 배우게 되는 알고리즘은 데이터를 일련의 명령이나 반복되는 절차에 의해 정렬을 수행하는 정렬 알고리즘이다.
세 가지의 알고리즘을 설명할 것이다.
버블 정렬, 삽입 정렬, 퀵 정렬
콩쥐에게 텍스트 에디터와 C 컴파일러만 설치된 컴퓨터(1초에 200회만의 연산이 간으한 고물)와, 3만 명이나 되는 학생들의 성적 데이터를 CD에 담아 콩쥐에게 건네주며
"내가 오늘 장에서 돌아올 때까지 석차 17,213등이 되는 학생의 번호를 알아내거라. 동점자는 한 사람도 없으니 금방 해낼 수 있겠지?"
라는 말을 하며 임무가 들어왔다 이 문제를 어떻게 해결해야 할까?
학생들 점수 오름차순으로 정렬한 다음, 목록에서 17,213번째를 고르면 된다.
정렬은 사전적으로 "물건 등을 가지런히 늘어 세우다"라는 뜻을 가지고 있다. 정렬의 궁극적인 목적은 깔금하고 보기 좋게 환경을 만드는 것도 답이 될 수 있지만, 찾으려고 하는 것을 쉽게 찾고자 하는 데에 있다.
정렬 알고리즘 역시, 데이터를 가지런히 나열하는 그 자체가 목적이 아니라 찾고자 하는 데이터를 빠르고 쉽게 찾을 수 있게 하는 것이 목적이다.
버블 정렬
:버블(Bubble: 거품) 정렬은 알고리즘이 데이터를 정렬하는 과정이 마치 물 속 깊은 곳에서 일어난 거품이 수면을 향해 올라오는 모습과 같다고 해서 붙여진 이름이다.
버블 정렬은 데이터 집합을 순회하면서 집합 내의 이웃 요소들끼리의 교한을 통해 정렬을 수행한다.
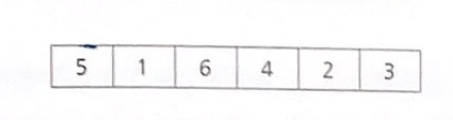
나열되어 있는 수의 집합을 오름차순으로 정렬해보자
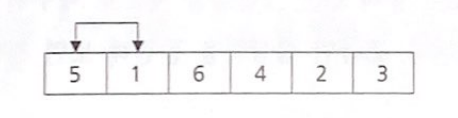

먼저 둘 사이를 비교하여 이웃끼리 올바른 순서로 위치해 있는지 확인 후 이웃 요소끼리 교환을 수행

1과 5비교 한 후 5에 있는 데이터가 더 크니 교환 수행
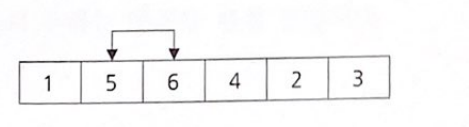
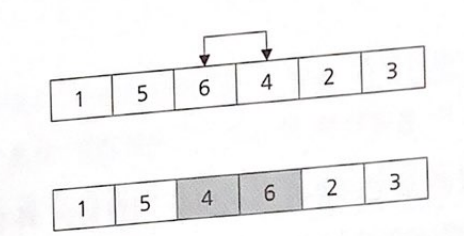

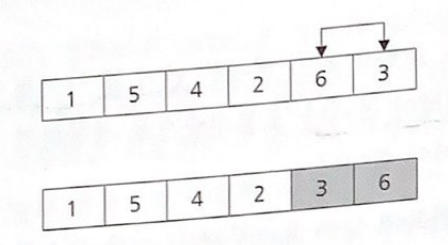
아직 정렬은 끝나지 않았다
가로로 놓여 있는 그림들을 세로로 세우면 6이 아래에서 뽀글거리며 올라가는 것처럼 보인다.
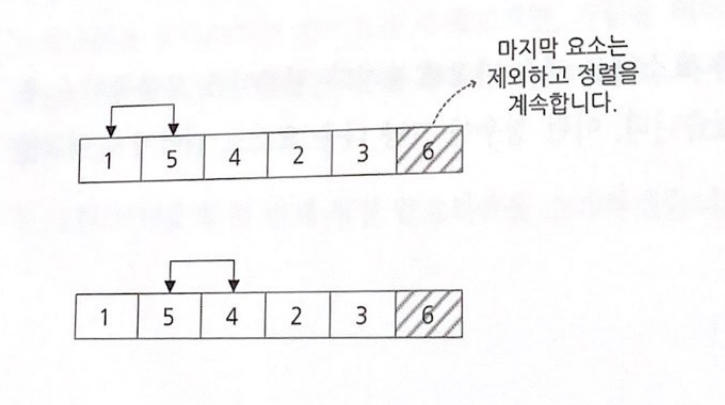
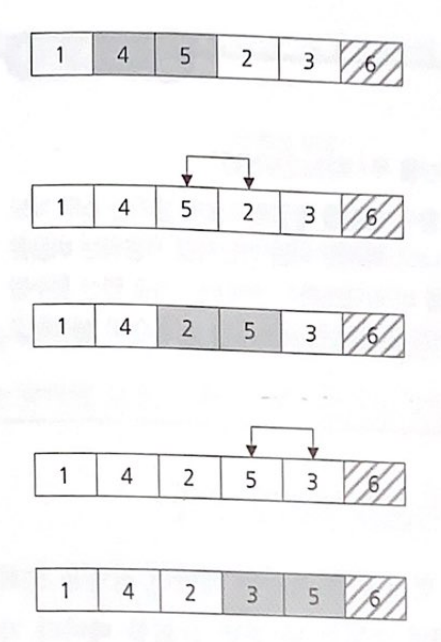
6과 5는 고정 시키고 이들을 제외한 나머지 데이터 집합에 대해 버블 정렬을 계속 수행하면, 결국에는 완전히 정렬된 데이터 집합을 얻을 수 있다.
버블 정렬은 얼마나 빠를까?
콩쥐가 가진 컴퓨터는 초당 200회 연산이 가능한 컴퓨터이다.
즉 초당 200회 연산이 가능한 컴퓨터로 1시간 내에 그 학생을 찾으려면 1분에 12,000회(200x60초), 1시간에 720,000회(12,000 x 60분) 이내로 작업을 마무리할 수 있는 알고리즘이 필요하다. 하지만 버블 정렬하는 동안에는 작업 다 하지 못한다.
그렇다면 얼마나 느릴까?
버블 정렬의 데이터 집합을 순회하는 횟수를 알아보자.
버블 정렬은 데이터 집합을 한번 순회할 때(한번 순회 할때마다 가장 큰 값이 가장 위에 놓인다)마다 정렬해야 하는 데이터 집합의 범위가 하나식 줄어드므로, 데이터 집합의 범위를 n개라고 한다면 n-1만큼 반복하면 정렬이 마무리 된다.

정렬 대상 범위가 여섯 개 이므로 다섯 번 비교
따라서, 우리 예제에서의 총 비교 횟수는 모두 5+4+3+2+1=15가 된다.
일반화

식 정리
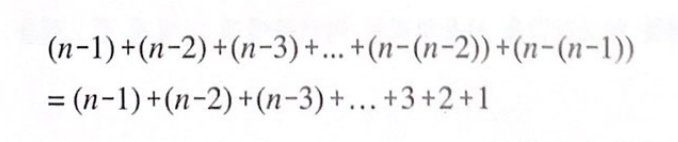
가우스 덧셈 활용
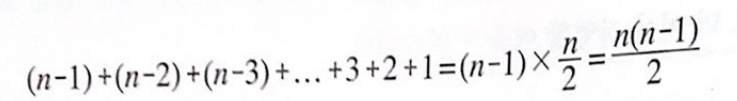
일반화 시킨 나온 공식이 버블 정렬의 횟수이다.
콩쥐가 다뤄야 하는 성적 데이터처럼 범위가 30,000개나 되는 데이터 집합을 정렬하는 경우에는 이야기가 달라진다. 약 450,000,000(4억 5천만)회의 비교 연산을 거쳐야 한다. 우리는 72만 번의 연산만으로 정렬을 끝내야 하는데, 버블 정렬은 콧방귀도 뀌지 않고 이 조건을 가볍게 무시한다.
삽입 정렬
:데이터 집합을 순회하면서 정렬이 필요한 요소를 뽑아내어 이를 다시 적당한 곳에 삽입해 나가는 알고리즘
쉽게 설명해보자
:뒤섞여 있는 트럼프 카드를 순서대로 정리하는 모습을 생각하면 이해가 쉽다. 카드를 한 장씩 뽑아 카드의 값에 따라 적절한 곳에 끼워 넣는 것을 반복하다 보면 결국에는 모든 카드가 순서대로 정리되는 것처럼, 데이터 집합에서 요소를 하나씩 뽑아 적절한 곳에 끼워 넣는 것을 반복하다 보면 정렬된 데이터 집합을 얻을 수 있다.
이 알고리즘은 구체적으로 다음의 과정을 통해 정렬을 수행한다. 정렬 방향은 오름차순이다.
1)데이터 집합에서 정렬 대상이 되는 요소들을 선택한다. 이 정렬 대상은 왼쪽부터 선택해나가며, 그 범위가 처음에는 2개지만, 알고리즘 반복 횟수가 늘어날 때마다 1개씩 커진다. 정렬 대상의 최대 범위는 '데이터 집합의 크기 -1'이 된다.
2)정렬 대상의 가장 오른쪽에 있는 요소가 정렬 대상 중 가장 큰 값을 가지고 있는지 확인한다. 만약 그렇지 않다면, 이 요소를 정렬 대상에서 뽑아내고, 이 요소가 위치할 적절한 곳을 정렬 대상 내에서 찾는다. 여기서 적절한 곳이라 함은, 데이터 집합의 가장 왼쪽을 기준으로 했을 때 자신보다 더 작은 요소가 없는 위치를 말한다.
3)뽑아 든 요소를 삽입할 적절한 곳을 찾았다면, 정렬 대상 내에서 삽입할 값보다 큰 값을 갖는 모든 요소를 한 자리씩 오른쪽으로 이동시키고(이러면 요소가 뽑힌 자리가 채워지고, 새로이 위치할 곳이 비워진다.), 새로 생긴 빈 자리에 삽입시킨다.
4)전체 데이터 집합의 정렬이 완료될 때까지 1~3을 반복한다.

우선 앞의 두 장의 카드를 정렬 대상으로 선택한다. 그리고 선택한 두 자으이 카드 중 오른쪽 카드가 왼쪽보다 큰지 비교한다. 왼쪽이 5, 오른쪽이 1, 오른쪽 카드가 작다. 그럼 1 카드를 뽑는다

뽑아낸 1은 5보다 앞에 와야한다. 1이 들어갈 자리를 만들기 위해 5를 오른쪽으로 한 자리 옮긴다.

그리고 5가 이동하여 생긴 빈자리에 1을 삽입 첫 번째 반복 끝

이번엔 정렬 대상의 범위를 하나 더 늘려서 크기가 3개가 됨.
마지막 요소가 6임 바로 앞에 있는 5와 비교해보니 6은 그자리에 있는 것이 옳다. 그 이전 요소들은 이미 정렬을 거친 상태이기 땨문에 더 이상 비교할 필요가 없다.

이번엔 정렬 대상의 마지막 요소 4이다. 바로 앞에 있는 6보다 작다. 4를 뽑는다.

4가 들어갈 곳은 5 앞이다. 정렬 대상 중 4보다 큰 5, 6을 오른쪽으로 한 자리씩 옮긴다.
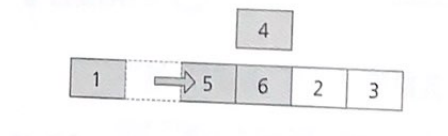
빈 자리에 4를 삽입. 이렇게 두 번만 더 반복하면 이 데이터 집합은 완전히 정렬된다.

정렬 대상을 줄여나가는 버블 정렬과는 반대로, 삽입 정렬은 정렬 대상을 하나씩 늘려간느 방식으로 한다.
삽입 정렬은 버블 정렬보다 빠를까요?
우리가 다룬 데이터 예제 6개, 정렬을 위한 반복은 5회 수행 그리고 데이터 집합 내 요소들간의 비교는 정렬 대상의 범위가 2개일 때 한 번, 3개일 때 두 번, 4개일 때 세 번, .... 그리고 6개일 때 5번 수행.
즉 삽입 정렬의 비교 횟수를 계산하면

비교 횟수가 버블 정렬과 같다. 하지만 위 공식과 우리가 다룬 데이터는 차이가 있다.
[1, 5, 6, 4 ] 정렬 과정 > 4를 뽑았을 때 두 번 비교함.
[1, 5, 6] 정렬 과정 > 한 번만 비교를 수행함.
버블 정렬은 반드시

만큼 비교를 거친다.
삽입 정렬은 데이터 집합이 정렬되어 있는 경우에는 한번도 비교를 거치지 않는다. 데이터 집합이 정렬되어 있는 최선의 경우와 역으로 정렬되어 있는 최악의 경우에 삽입 정렬이 수행하는 비교 횟수의 평균을 낸다면
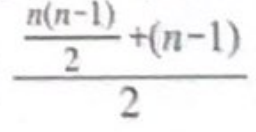
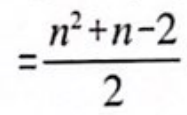
평균적으로 삽입 정렬이 더 나은 성능을 보인다.
여튼 콩쥐에게는 30,000개의 데이터에 대해 72만 번의 비교만으로 정렬을 완료할 수 있는 알고리즘이 필요
평균 비교횟수 삽입 정렬은 225,007,499(2억 2천 5백만 7천 4백구십구)회 비교를 수행
아직 부족하다
퀵 정렬
:퀵 정렬(Quick Sort)은 전쟁 전략 중의 하나인 '분할 정복(Divide and Conquer)'에 기반한 알고리즘이다. 분할 정복 전략은 적군의 전체를 공략하는 대신, 전체를 구성하는 구성 요소들을 나누어 잘게 쪼개진 적을 공략하는 전법이다.
퀵 정렬은 분할 정복을 이용해 정렬을 수행합니다.
1. 데이터 집합 내에서 임이의 기준 요소를 선택하고, 기준 요소보다 작은 요소들은 순서에 관계없이 무조건 기준 요소의 왼편에, 큰 값은 오른편에 위치한다.
2. 기준 요소 왼편에는 기준 요소보다 작은 요소들이 모여 있고 오른편에는 큰 요소들이 모여 있다. 이렇게 나눈 데이터 집합들을 다시 1에서와 같이 임의의 기준 요소를 선택하고 같은 방법으로 데이터 집합을 분할합니다.
3.1과 2의 과정을 더 이상 데이터 집합을 나눌 수 없을 때까지 반복하면 정렬된 데이터 집합을 얻게 된다.
먼저 기준 값을 선택. 기준 요소를 선택하는 방법에는 여러 가지 있다, 하지만 우리는 데이터 집합의 첫 번째 요소를 사용하겠다. 5가 기준이 된다.

요소 5를 기준으로, 5보다 작은 요소들은 왼쪽에, 큰 요소들은 오른쪽에 '닥치는 대로' 모은다. 이 결과로 왼쪽과 오른쪽에 정렬되지는 않았지만, 범위가 한정되어 있는 데이터 집합이 생긴다.
이렇게 생긴 왼쪽과 오른쪽의 데이터 집합에 대해 분할 수행을 한다. 왼쪽이든 오른쪽이든 어느 쪽을 먼저 해도 상관은 없다. 우리는 왼쪽부터 분할해보겠다.
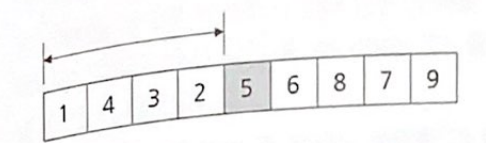
분리를 위해서는 먼저 기준 요소를 선택해야 한다는 사실을 기억하자. 가장 처음에 있는 요소 1을 기준으로 지정한다.

그런데 1, 4, 3, 2 중에 1보다 작은 요소는 없다. 1보다 큰 요소는 모두 오른쪽에 와 있어서 이미 분할되어 있는 상태이다. 이번엔 이제 새로 생긴 오른쪽으 데이터 집합 4, 3, 2에 대해 분할을 수행한다.
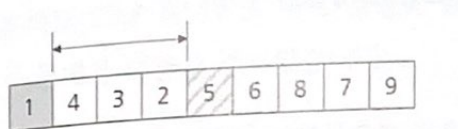
4, 3, 2 중에 첫 번째인 4를 기준 요소로 선택하여 분할 수행
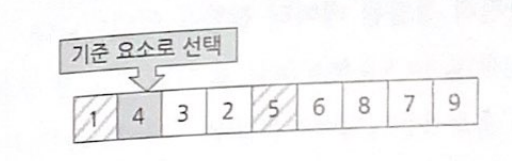
4보다 큰 요소는 하나도 없고 모두 작은 요소들뿐이다. 분할 결과로 왼쪽에만 데이터 집합이 생겼다. 이제 3, 2에 대해 분할을 해보자.
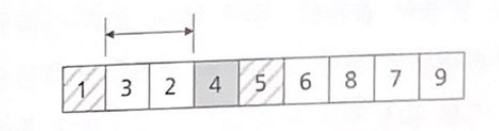
3, 2 중 첫 번째에 위치한 3을 선택하여 분할을 수행한다.
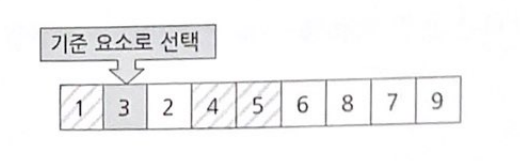
2는 3보다 작으니 3의 왼쪽으로 와야한다. 이렇게 해서 최초의 분할에서 생긴 왼쪽 데이터 집합이 모두 정렬되었다. 남아있는 오른쪽 데이터 집합의 분할을 계속해보자.

6을 기준 요소로 선택했는데, 6보다 작은 요소가 없다. 이대로 6의 오른쪽에 있는 데이터 집합에 대해 분할을 수행한다.
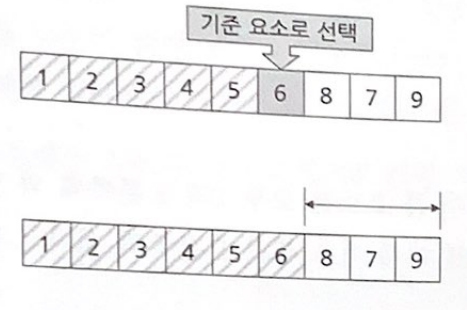
8, 7, 9 중 8선택 분할 수행

더 이상 분할할 수 없는 단계에 왔다. 완전히 정렬된 데이터 집합을 얻었다.
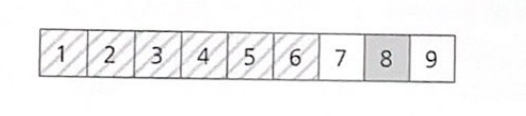
퀵 정렬이 퀵 정렬을 호출한다.
두 가지 문제가 있다.
1.배열을 데이터 집합의 자료구조로 사용할 때, 분할은 어떻게 수행해야 하는가?(링크드 리스트처럼 삽입/삭제가 자유롭지 못하므로)
2.반복되는 분할 과정을 어떻게 처리할 것인가?
첫 번째 문제를 살펴보자
'수색 섬멸' 작전을 사용해보자.
정찰병 2명을 투입
한 명은 왼쪽부터 오른쪽 방향 데이터 집합 검사하면서 기준보다 큰 요소를 찾는다.
한 명은 오른쪽부터 왼쪽 방향으로 검사하면서 기준보다 작은 요소를 찾는다.
이 두 정찰병이 찾아낸 두 요소를 교환하는 것이다. 그리고 정찰병들은 서로 접선할 때까지 검사를 계속 진행하면서 교환해야 될 요소를 찾아내고 교환을 수행한다.
두 정찰병이 접선하면 기준 요소를 왼쪽 데이터 집합의 마지막 요소와 교환하는 것으로 종료한다.
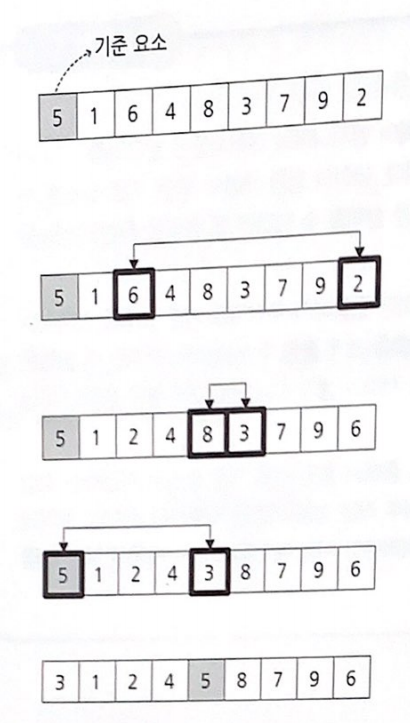
두 번째 문제를 살펴보자
이 문제의 요지는 '반복되는 분할 과정을 어떻게 프로그래밍하느냐'인데 다음 문장을 읽어보고 이 문장 속에 담긴 내용을 머릿속으로 그려보자
"콩쥐가 콩쥐팥쥐전을 읽는다. 책의 내용은 콩쥐가 콩쥐팥쥐전을 읽는다는 것이다"
무슨 말장난이냐 즉 콩쥐는 콩쥐팥쥐전을 읽으면서, 그 책 안에 있는 자신을 반결할 것이다. 그런데 책 속의 자신도 콩쥐팥쥐전을 읽고 있을 것이다. 책 소그이 책속의 콩쥐도 또 콩쥐팥쥐전을 읽고 있다. C 언어는 함수 내에서 함수 자신을 호출하는 '재귀 호출' 기능을 제공한다. 재귀 호출을 이용하여 반복되는 분할 과정을 처리할 것이다.
퀴 정렬은 빠릅니다!
버블 정렬과 삽입 정렬은 비교 횟수와 데이터 집합을 순회하는 반복 횟수를 이용해서 성능 분석을 했다. 퀵 정렬도 이 알고리즘처럼 비교에 근거한 방법을 취하기 때문에, 성능 분석에는 비교 횟수가 필요하다. 다른 점이라면 반복 횟수 대신 재귀 호출의 '깊이'를 이용한다는 사실이다.
- 퀵 정렬의 재귀 호출 깊이
- 데이터 집합을 나누기 위해 필요한 비교 횟수
최선의 경우
퀵 정렬은 데이터 집합이 어떻게 정렬되어 있는지가 좌우하는 알고리즘이다.
데이터가 미리 정렬되어 있거나 또는 역순으로 정렬되어 있는 경우에는 최악의 성능을 보입니다. 하지만 데이터 요소들이 이리저리 흩어져 있는 경우에는 최고의 성능을 자랑한다.
다음 그림은 로또 1등에 당첨될 확률보다 더 만나기 어려운, 퀵 정렬에게 있어 가장 '이상적인' 모습의 데이터 집합을 분할하는 과정이다.

퀵 정렬이 한번 호출될 때마다 데이터 집합이 1/2 쪼개진다. 비록 꿈에서나 만날 수 있는 상황이긴 하지만, 위 상황을 토대로 성능 분석을 해 보겠다.
한 덩어리를 한 번에 두 조각으로 나눠서 마지막에 8개의 조각이 되게 만드려면 세 단계에 이르는 재귀 호출을 거쳐야 한다. 16개의 조각으로 만들기 위해서는 네 단계의 재귀 호출을 거쳐야 하고, 32개의 조각으로 나누려면 다섯 번의 재귀 호출이 필요하다.
우리는 여기에서 한 가지 규칙을 찾을 수 있다. 그 구칙은 '데이터 집합의 크기가 n개 일 때, 퀵 정렬의 재귀 호출 깊이는 log2n이다' 라는 사실
로그를 배워보자

재귀 호출의 깊이는 알아냈다. 이제 비교 횟수만 알아내면 된다.
매 단계에서 쪼개져 있는 각 데이터 집합의 크기를 합하면 항상 n개 된다.
따라서 이상적인 경우에 퀵 정렬의 성능은 다음과 같이 정리할 수 있다.

콩쥐 생각해보자
30000 x log2(밑) 30000 = 446180.25 45만 회가 채 안 되는 비교를 수행하며 데이터를 모두 정렬할 수 있다.
최악의 경우

최악의 경우를 만나면 위 그림 만큼 비교를 수행해야하는데
왜 이 만큼일까?

다음 그림과 같이 재귀 호출마다 데이터 집합의 분할이 1 : n-1로 이루어진다.
이렇게 되면 재귀 호출의 깊이는 n-1이 되고, 매 재귀 호출이 일어날 때마다 정렬 대상의 범위도 1씩 줄어든다.
따라서 최악인 경우 퀵 정렬의 총 비교 횟수는

이렇게 정리된다.
최악의 경우에는 버블 정렬이나 삽입 정렬의 성능과 비슷해진다고 할 수 있다. 하지만 이런 경우는 최선의 경우와 마찬가지로 아주 드물므로 큰 걱정하지 마라.
평균의 경우
퀵 정렬은 평균적으로 1.39nlog2(밑)n회 비교를 수행한다. 이것은 nlog2(밑)n인 최선의 경우에 비해 39%정도만 느린 것이다.

콩쥐에게 준 성적 데이터의 산포가 평균적이라고 한다면, 콩쥐가 가진 문제를 620190.54회만 비교해도 풀 수 있다.
'Algorithm > 뇌를 자극하는 알고리즘' 카테고리의 다른 글
| 4장 트리 (1) | 2022.02.02 |
|---|---|
| 3장 큐 (0) | 2022.02.02 |
| 2장 스택 (0) | 2022.02.01 |