프로시저란, 한 컴퓨터 프로세스가 어떻게 나아가는지, 곧 지난 일을 발판 삼아 다음으로 해야 할 일을 밝힌 것이다.
이 절에서는 단순한 프로시저가 만들어 내는 프로세스 가운데 자주 나타나는 몇 가지 '꼴'을 보기로 들어서 살펴보려고 한다. 아울러 그런 프로세스가 쓰는 계산 자원, 곧 시간과 공간 자원이 어떤 비율로 늘어나는지도 따저볼 참이다.
1.2.1 되돌거나 반복하는 프로세스
사다리곱 함수

맞바꿈 계산법에 따라 식이 옆으로 펼처진 다음에 다시 줄어드는 꼴을 볼 수 있다. 프로세스가 곧바로 연산을 하지 않고 자꾸 미루어 놓는 탓에 식이 옆으로 늘어나다가, 곱셈 연산을 하면서 줄어들기 시작한다. 이처럼 곧바로 셈하지 못하고 미루어 놓는 연산이 끈처럼 이어지는 게 되도는 프로세스의 특징이다. 이런 프로세스를 돌릴 때, 실행기는 미뤄둔 연산을 모두 쥐고 있다가 다시 되밟을 수 있도록 해야 한다. n! 값을 ㅜ하면서 미루어 둔 곱셈 끈의 길이, 곧 실행기가 쥐어야 할 정보의 크기는, 셈하는 데 거치는 단계 수와 마찬가지로 n에 비례하여 나란히(선형으로) 자라난다. 이런 프로세스를 두고 선형 재귀 프로세스라 한다.

이 프로세스는 늘거나 줄지 않는다. n의 크기와 관계없이 product, counter, max-count 변수에 단계마다 구한 값만 넣어주면 그만이다. 이것을 반복하는 프로세스라 하는데, 보통 반복하는 프로세스에는 정해진 상태변수가 있어서 반복할 때마다 바뀌는 계산 상태를 간추려서 기록해둘 수 있고, 계산 단계가 넘어갈 때마다 상태변수 값을 고쳐 쓰는 규칙이 있으며, 계산을 끝낼 조건을 따지는 마무리 검사 과정도 있다. 이 보기에 앞서 보듯이, n!값을 구하는 데 거치는 단계 수가 n에 비례하여 나란히 자라날 때, 이런 프로세스를 선형 반복 프로세스라 한다.
1.2.2 여러 갈래로 되도는 프로세스
여러 갈래로 되돌기를 들 수 있다. 이 프로세스를 설명하기 이해 피보나치 수열로 해보자

이 정의에 따라 프로시저를 만들면 아래처럼 되도는 프로시저가 만들어진다

이 프로시저가 어떤 식으로 계산되는지 보자. 정의대로 구한다.

이 그림처럼 나무꼴로 펄쳐지고, 단계마다 가지가 둘씩 갈라져 나온다. 즉 fib 프로시저는 한 번 불릴 때마다 자기를 두 번 부른다. 같은 계산을 쓸데없이 반복하기 때문에 피보나치 수열을 구하기에는 별로 좋지 않는 방법이다.
반복으로 프로세스로 구해보자

둘 다 같은 일을 하지만, 계산 단계 수가 n에 선형 비례로 자라나는 방법과 Fib(n)에 비례하여 자라나는 방법은, 입력의 크기가 작다 해도 그 결과가 엄청나게 다르다. 그러나 여기서 보기로 든 프로세스만 가지고 여러 갈래로 되도는 프로세스가 아무 짝에도 쓸모없는 것이라고 말해서는 안 된다. 수가 아니라, 계층 구조 데이터를 다루는 프로세스에서는 여러 갈래로 되도는 규칙이 아주 쓸모 있고 잘 들어맞을 때가 있다. 또 수를 셈하는 문제라 하더라도, 문제를 이해하고 프로그램을 설계할 때에는 여러 갈래로 되도는 프로세스가 크게 도움이 된다. 피보나치 수열을 구하는 문제에서도 처음 만든 fib 프로시저가 다음에 만든 것보다 훨씬 성능이 떨어지기는 하지만, 처음 짠 프로시저는 피보나치 수열의 수학 정의 그대로 Lisp로 옮겼다고 봐도 될 만큼 그 정의가 쉽게 와 닿는다. 다만, 반복하는 알고리즘으로 fib 프로시저를 짤 때에는 상태변수 세 개를 왜 따로 만들어 써야 하는지 반드시 짚고 넘어가야 했다.
1.2.3 프로세스가 자라나는 정도
어떤 프로세스냐에 따라 계산 자원을 쓰는 크기가 달라진다. 그 차이를 서로 견주고 싶을 때, 프로세스가 자라나는 정도라는 개념을 쓰면 되는데, 이는 입력의 크기에 따라 프로세스가 쓰는 자원양이 자라나는 정도를 말한다.
문제의 크기를 매개변수 n, n만큼 큰 문제를 푸는 데 드는 자원양을 R(n)
컴퓨터에서는 한 번에 처리할 수 있는 연산 수가 정해져 있기 때문에, 계산하는 데 드는 시간은 그 계산에서 쓰는 기계 연산 수에 비례할 것이다.

n이 알맞게 큰 값을 가리키는 변수이고, n에 매이지 않은 상수 k1 과 k2가 다음 조건을 만족한다면, R(n)은 ⊙(f(n)) 차수로 자라난다고 하고, R(n) = ⊙(f(n))이라고 쓰며 'theta of f(n)'라 읽는다.
사다리곱을 계산할 때 썼던 되도는 프로세스에서는, 그 계산 단계가 n에 비례하여 늘어났다. 그러므로 이 프로세스가 거쳐야 할 단계는 ⊙(n)만큼 늘어나고, 계산에 필요한 기억 공간도 ⊙(n)으로 자라났다. 한데, 반복하는 프로세스로 사다리곱을 구하는 경우, 단계가 ⊙(n)으로 늘어난다는 점은 되도는 프로세스와 같다.
''''''책 읽어보자'''''
1.2.4 거듭제곱
같은 수를 여러 번 곱하는 문제. 밑수 b, 0보다 큰 정수 n을 인자로 받아 b^n을 구하는 프로시만 만들면 쉽게 풀릴 문제.
이 문제 재귀 규칙

선형 재귀 프로세스

⊙(n)계산 단계를 거치며 ⊙(n)만큼 기억 공간 사용한다.
선형 반복 프로세스

⊙(n)계산 단계를 거치지만 기억 공간은 ⊙(1)사용.
계산 단계를 더 줄이기 위해서 계속 제곱하는 방법을 사용할 수 있다.
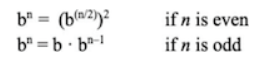

fast-expt 프로시저가 펼쳐내는 프로세스의 계산 단계(시간)와 필요한 공간은 n의 로그로 자라난다. 이 프로세스의 자람 차수는 ⊙(log n)이다. n이 커질수록 자람 차수 ⊙(log n)과 ⊙(n)의 차이는 엄청나게 벌어진다.
1.2.5 최대 공약수
정수 a와 b의 최대 공약수(GCD)란, 두 수를 나머지 없이 잘라 나눌 수 있는 가장 큰 정수를 말한다.
두 정수의 GCD는 인수 분해로도 구할 수 있으나, 그보다 훨씬 좋다고 알려진 알고리즘으로도 구할 수 있다.
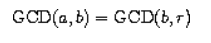
이 계산법에 따르면 a와 b의 GCD를 구하는 문제는 그보다 적은 두 수 b와 r의 GCD를 구하는 문제로 줄어드는 과정을 밟아간다.

끝내 2가 나오게 되고, 0보다 큰 정수 둘을 받아서 이런 과정을 되풀이하면 언제나 둘째 수가 0이 된다., 이때 첫 수가 GCD다. 이것을 유클리트 알고리즘이라 한다.
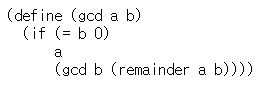
이 프로시저는 반복하는 프로세스로 펄쳐지면, 밟아야 할 단계 수가 로그 비례로 자라난다.
람의 정리를 통해 유클리트 알고리즘의 자람 차수를 얻을 수 있다.
라메의 정리(Lame's Theorem): 유클리드 알고리즘으로 GCD를 구하는 데 k단계를 거치는 경우, 두 수 가운데 작은 수는 k번째 피보나치 수보다 크거나 같아야 한다.
이로 인해 자람 차수는 ⊙(log n)이다.
1.2.6 연습: 소수 찾기
정수 n이 소수인지 알아보자
약수 찾기

수 n의 약수 가운데(1보다 큰) 가장 작은 약수를 구하는 프로그램으로, 2부터 이어지는 정수를 차례로 살펴서 n의 약수가 되는지 따져보는 간단한 방법을 쓴다.
수 n의 가장 작은 약수가 n뿐일 때, 이 n을 소수라 할 수 있기 때문에, 이런 생각에 따라 프로시저를 정의하면 다음과 같다.
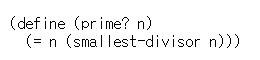
find-divisor를 끝내는 조건은, n이 소수가 아니라면 루트n 보다 작거나 같은 약수가 꼭 있다는 사실에 바탕을 둔다. 곧, 이 알고리즘은 1부터 루트n 사이 값만 따져 보면 된다. 그러므로 n이 소수인지 알아보는 데 거치는 계산 단계는 ⊙루트 n이다.
페르마 검사
⊙(log n) 차수로 소수를 찾는 방법은 '페르마의 작은 정리' 라고 하는 이론에서 이끌어 낸 알고리즘.
페르마의 작은 정리: n이 소수고, a가 n 보다는 작고 0보다는 큰 정수라면, a^n은 a modulo n으로 맞아떨어진다.
'컴퓨터 프로그램의 구조와 해석 > 1장 프로시저를 써서 요약하는 방법' 카테고리의 다른 글
| 1.3 차수 높은 프로시저로 요약하는 방법 (0) | 2022.02.02 |
|---|---|
| 1.1 프로그램 짤 때 바탕이 되는 것 (0) | 2022.01.30 |