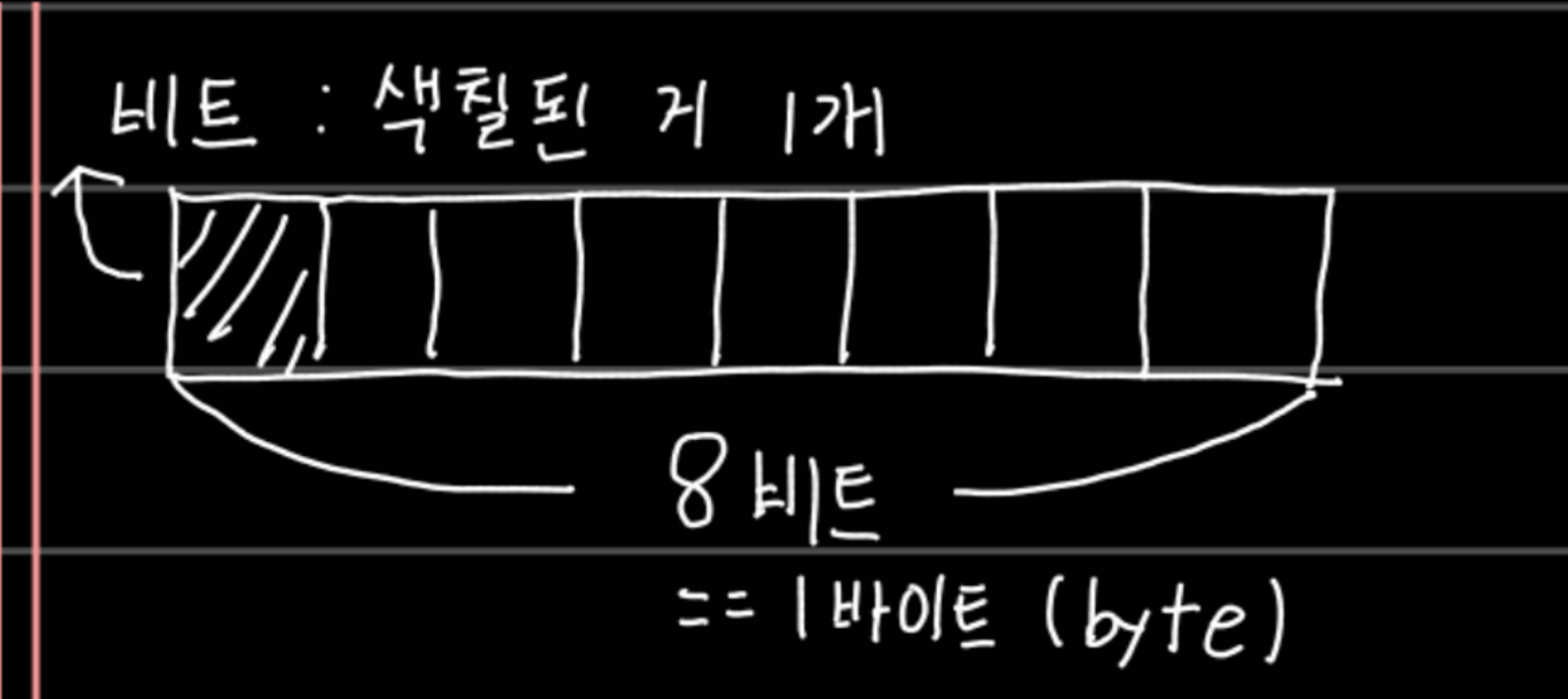
이 글은 이 분의 블로그 통해 공부한 글입니다. 이진 기수법을 통한 고정 소수점(Fixed Point) 와 부동 소수점(Floating Point) 이진 기수법을 통한 고정 소수점(Fixed Point) 와 부동 소수점(Floating Point) 이 글은 제가 공부하기 위해 여러 사전이나, 책, 그리고 다른 개발자 분의 내용을 타이핑하여 학습한 내용이므로, 이 원본은 출처를 꼭 남깁니다. 원래내용과 살짝 다를 수 있는 점 양해바랍니다 daldalhanstory.tistory.com 이진 기수법(이진법에 대한 내용을 좀 더 자세하게 알고 싶으면 나의 블로그 밑 부분의 개념을 보고 오자 https://wo-dbs.tistory.com/141 이진 기수법(이진법) 컴퓨터는 0과 1로 이루어진 기계어를 사용한..